The classes McMd::NvtLangevinIntegrator and DdMd::NvtLangevinIntegrator compute approximate solutions to the Langevin equation. This page describe the time stepping algorithm used by both of these classes.

See also: McMd::NvtLangevinIntegrator; DdMd::NvtLangevinIntegrator

Langevin Equation

The Langevin equation for each particle is given by Newton's equation

$m\frac{d{\bf v}}{dt} = {\bf f}$

with a force

${\bf f} = -\frac{\partial U}{\partial {\bf r}} - m\gamma {\bf v} + {\bf f}^{\rm (r)} ,$

that includes frictional and random components, in which:

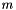is the particle mass
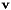${\bf v}$ is the particle velocity
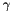$\gamma$ is a velocity relaxation rate (inverse time) parameter
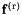${\bf f}^{\rm (r)}$ is a random force.

The random force must have a mean and auto-correlation function:

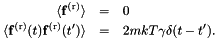
$\begin{eqnarray*} \langle {\bf f}^{\rm (r)}\rangle & = & 0 \\ \langle {\bf f}^{\rm (r)}(t) {\bf f}^{\rm (r)}(t') \rangle & = & 2 m kT \gamma \delta (t-t') . \end{eqnarray*}$

Integration Algorithm

The algorithm uses a conventional two-step velocity-Verlet time stepping sequence, identical to that of of the energy conserving NVE integrators, with a modified total force. This algorithm uses the following two-step update scheme for the velocity 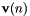${\bf v}(n)$ and position ${\bf r}(n)$ :

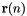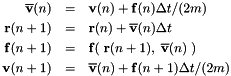
$\begin{eqnarray*} \overline{\bf v}(n) & = & {\bf v}(n) + {\bf f}(n) \Delta t /(2m) \\ {\bf r}(n+1) & = & {\bf r}(n) + \overline{\bf v}(n)\Delta t \\ {\bf f}(n+1) & = & {\bf f}(\;{\bf r}(n+1),\; \overline{\bf v}(n)\; ) \\ {\bf v}(n+1) & = & \overline{\bf v}(n) + {\bf f}(n+1)\Delta t /(2m) \\ \end{eqnarray*}$

The total force 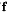${\bf f}$ is given by a function

${\bf f}(n+1) = {\bf f}^{\rm (pot)}(n+1) + c_{v}\overline{\bf v}(n) + c_{r}{\bf u}(n+1),$

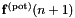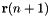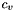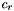in which ${\bf f}^{\rm (pot)}(n+1)$ is the conservative force derived from the potential energy, evaluated at updated position ${\bf r}(n+1)$ , $c_{v}$ and $c_{r}$ are numerical coefficients whose values are determined below, and 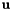${\bf u}$ is a dimensioness random number whose Cartesian components are each uniformly distributed random numbers in the range $[-1/2, 1/2]$ .

Because the force 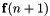${\bf f}(n+1)$ is calculated between the first step of this two-step integrator (i.e., first two lines of the above algorithm) and the final velocity update (the last line), it contains a conservative force that is calculated using fully updated positions 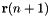${\bf r}(n+1)$ but a frictional drag force calculated using the half-updated velocity 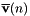$\overline{\bf v}(n)$ . In practice, the drag and random forces for each particle are evaluated and added to the total force for that particle at the beginning of the loop over particles for second step of the algorithm, after evaluation of the conservative forces for all particles.

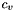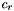Determination of Coefficients: The coefficients $c_{v}$ and $c_{r}$ are chosen so that in the absence of any potential force (i.e., in an ideal gas) the algorithm would yield the exact result for the decay of velocity correlations and for the variance of the velocity obtained at the end of each step. In an ideal gas, the velocity change between midstep force evaluations is given by

$\overline{\bf v} (n+1) = ( 1 + c_{v} \Delta t/m )\overline{\bf v}(n) + (c_{r}\Delta t/m) {\bf u}$

By convention, we choose the constant 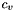$c_{v}$ such that 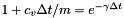$1 + c_{v}\Delta t/m = e^{-\gamma\Delta t}$ , where 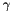$\gamma$ is a decay rate parameter input by the user. This yields the decay of velocity auto-correlations between midstep velocities predicted by the exact solution. This gives a coefficient

$c_{v} = -m (1 - e^{-\gamma\Delta t})/\Delta t ,$

for which 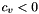$c_{v} < 0$ . The coefficient 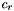$c_{r}$ for the random force is then chosen so that, in the absence of conservative forces, the mapping would produce a variance for the end of step velocities that satisfies the equipartition theorem

$\langle v_{i} v_{j} \rangle = \delta_{ij} k_{B}T/m ,$

Because there are systematic differences between the mid-step and end-of-step velocities, this turns out to imply that the mid-step velocities obey a modified equation

$\langle \overline{v}_{i} \overline{v}_{j} \rangle = \delta_{ij} d k_{B}T/m .$

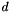in which $d$ is a coefficient that approaches unity only in the continuum limit 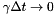$\gamma\Delta t \rightarrow 0$ . Applying the above criteria for the variance of the midstep velocities, while treating 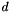$d$ for now as unknown, and using the identity 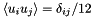$\langle u_{i} u_{j} \rangle = \delta_{ij}/12$ for the Cartesian components of 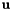${\bf u}$ , we obtain:

$c_{r} = \sqrt{12 m k_{B}T d ( 1 - e^{-2\gamma\Delta t})}/\Delta t$

To determine 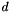$d$ , we then use the mapping

${\bf v}(n+1) = [1 + c_{v}\Delta t/(2m)] \overline{\bf v}(n) + [c_{r} \Delta t/(2m)] {\bf u}(n+1)$

for an ideal gas to calculate the relationship between variances for midstep and final velocities, and require that the end-of-step velocities satisfy equipartition. This yields:

$d = 2/(1 + e^{-\gamma\Delta t}) .$

Substituting this into the equation for 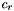$c_{r}$ completes the specification of constants in the algorithm.

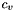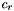Because the values of the coefficients $c_{v}$ and $c_{r}$ depend on the particle mass, values must be calculated for each atom type. These values are stored in private arrays named cv_ and cr_ that are indexed by atom type id.