Detailed Description

Potential functions for covalent dihedral interactions.

Dihedral potentials are usually expressed as functions of a dihedral torsion angle, 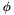$\phi$ . Dihedral interactions may use instances of Torsion and TorsionForce to calculate the dihedral angle and its derivatives. The dihedral angle is defined in these classes as follows:

Consider 4 sequential atoms with position vectors 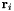${\bf r}_{i}$ labelled sequentially by an index i = 0, 1, 2, 3. We define three bond vectors

${\bf b}_i = {\bf r}_i - {\bf r}_{i-1}$

for i = 1, 2, 3. The dihedral angle is an angle between the plane spanned by bond vectors 1 and 2 and the plane spanned by bond vectors 2 and 3. Define two vectors

${\bf v}_{1} = {\bf b}_1 \times {\bf b}_2 \quad\quad {\bf v}_{2} = {\bf b}_2 \times {\bf b}_3$

perpendicular to these planes, and corresponding unit vectors

${\bf u}_1 = {\bf v}_{1}/|{\bf v}_{1}| \quad\quad {\bf u}_2 = {\bf v}_{2}/|{\bf v}_{2}|$

The cosine of the dihedral angle is given by the dot product:

$\cos(\phi) \equiv {\bf u}_1 \cdot {\bf u}_2$

With this convention, a planar cis (arc) conformation yields phi = 0, and a planar trans (zig-zag) conformation yields phi = 180 degrees.

Classes
class	Simp::CosineDihedral
	A dihedral potential proportional to cos(phi). More...

class	Simp::MultiHarmonicDihedral
	A truncated Fourier series dihedral potential. More...

struct	Simp::Torsion
	Computes dihedral / torsion angle involving 3 bonds. More...

struct	Simp::TorsionForce
	Computes derivatives of dihedral angle with respect to bond vectors. More...

Detailed Description

Classes