Each of the angle interaction classes defines a potential that depends upon the angle between two bonds that connect three atoms. Each such group of atoms is assigned an angle type index, values of the parameters in the angle potential function are used for different angle types.

All of the angle interaction classes implement a common interface, which is described here.

Geometry

Let the three atoms in an angle group be labelled 0, 1, 2, with bonds connecting 0-1 and 1-2. Let 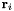${\bf r}_{i}$ be the position vector for atom i, with 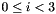$0 \leq i < 3$ . We define two bond vectors

${\bf b}_{1} \equiv {\bf r}_{1} - {\bf r}_{0} \quad\quad\quad\quad {\bf b}_{2} \equiv {\bf r}_{2} - {\bf r}_{1}$

The energy is assumed to be a function of the central angle 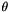$\theta$ , defined such that

$\cos(\theta) = \frac{{\bf b}_{1} \cdot {\bf b}_{2}} {|{\bf b}_{1}||{\bf b}_{2}|}$

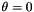so that $\theta = 0$ corresponds to a three atoms placed sequentially along a line.

Angle Interaction Classes

CosineAngle - proportional to the cosine of the bending angle
CosineSqAngle - proportional to the square of cosine of bending angle
HarmonicAngle - harmonic in bending angle