The LJPair interaction (pairstyle LJPair) implements a cutoff and shifted Lennard-Jones interaction. The potential energy 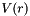$V(r)$ for a pair of nonbonded particles separated by a distance 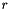$r$ is given for each pair of atoms types by a function

$V(r) = 4 \epsilon \left [ \left ( \frac{\sigma}{r} \right )^{12} - \left ( \frac{\sigma}{r} \right )^{6} \right ] + s$

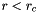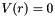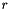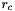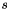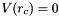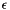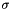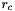for all $r < r_{c}$ , and vanishes ( $V(r) = 0$ ) for all $r$ greater than the cutoff distance $r_{c}$ . The constant shift $s$ is chosen for each pair of atom types such that $V(r_c) = 0$ . Different values are defined for the parameters $\epsilon$ , $\sigma$ and $r_{c}$ for each distinct pair of monomer types 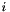$i$ and $j$ .

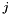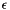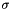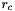Values of the parameters $\epsilon$ , $\sigma$ , and $r_{c}$ are denoted in the parameter file and source code by matrix-valued variables named "epsilon", "sigma", and "cutoff", respectively.

The parameter file format is:

epsilon  Matrix<float>
sigma    Matrix<float>
cutoff   Matrix<float>

All three parameter matrices are symmetric, and are entered in lower diagonal form. For example, for a system with two types of monomer, we might have:

epsilon   1.0      1.5
          1.5      1.0
sigma     1.0      1.0
          1. 0     1.0
cutoff    1.122    1.122
          1.122    1.122

The value of 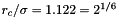$r_{c}/\sigma = 1.122 = 2^{1/6}$ used in the above yields a so-called Weeks-Chandler-Anderson potential, which is the potential that is obtained by cutting off and shifting the LJ potential at its minimimum.